Meteo Module

The METEO module was initially developed for simulations of meteotsnamis. It now includes subroutines for simulating the wind effects on waves, storm surges, landslide-generated tsunamis and processes related to atmospheric pressure effects.

Wind effect on waves

Wind effects are modeled using the wind stress forcing proposed by Chen et al. (2004). The wind stress is expressed by:

(115)\[{\bf R}_w = \frac{\rho_a}{\rho} C_{dw} |{\bf U}_{10} - {\bf C}| ({\bf U}_{10} - {\bf C})\]

where \(\rho_a\) and \(\rho\) represent air density and water density, respectively, and \(\bf C\) is wave celerity. The wind stress is only applied on wave crests. A free parameter representing the ratio of the forced crest height to maximum surface elevation is implemented in the model.

Holland model

The Holland model is an analytic model of wind and sea level pressure profiles of hurricanes (see Holland, 1980 for more information). The pressure distribution can be expressed by:

(116)\[p = p_c + (p_n-p_c) exp(-A/r^B)\]

where \(p\) is the pressure at radius \(r\), \(p_c\) and \(p_n\) are the central pressure and the ambient pressure, respectively, and \(A\) and \(B\) are scaling parameters from the model input. The velocity distribution can be described by:

(117)\[V_c = [AB(p_n-p_c)exp(-A/r^B)/\rho_a r^B]^{1/2}\]

Based on the formulations above, it is easy to obtain the following storm parameters:

The radius of maximum winds (RMW):

(118)\[R_w = A^{1/B}\]

The maximum wind speed:

(119)\[V_m = C(p_n-p_c)^{1/2}\]

where:

(120)\[C = (B/\rho_a e)^{1/2}\]

Storm surge

Storm surge is the additional water level generated by a storm (e.g., tropical cyclone) that exceeds the predicted astronomical tide. To calculate storm surges, wind stress is applied at the water surface:

(121)\[{\bf R}_w = \frac{\rho_a}{\rho} C_{dw} |{\bf U}_{10}| ({\bf U}_{10})\]

Note that \(\bf C\) is not used, compared to Eq. (115).

Meteotsunami

Meteotsunamis are modeled using a pressure source with a two-dimensional Gaussian distribution:

(122)\[P = dP exp \left(-(\frac{(x^\prime - x_0)^2}{2\sigma_x^2} + \frac{(y^\prime - y_0)^2}{2\sigma_y^2}) \right)\]

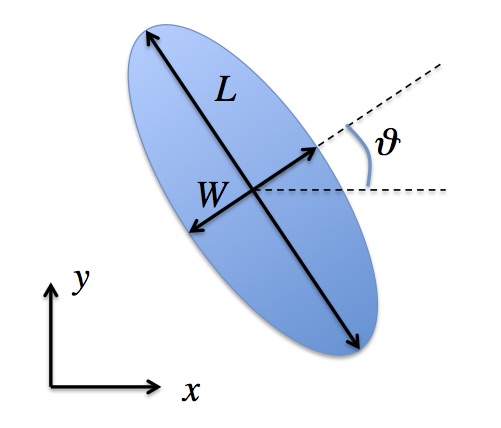
where \(dP\) is the pressure anomaly in mb, and \((x^\prime,y^\prime)\) are the coordinates rotated to the pressure moving direction (angle is \(\theta\) as indicated in the figure below). \(\sigma_x\) and \(\sigma_y\) are paramters representing the length and width of the pressure source, respectively.

Landslide-generated tsunami

Landslide-generated tsunamis can be calculated using the same approach as the meteotsunami. Details are reported by Woodruff et al. (2018).

References

Chen, Q., Kaihatu, J. M., & Hwang, P. A. (2004). Incorporation of wind effects into Boussinesq wave models. Journal of Waterway, Port, Coastal and Ocean Engineering, 130(6), 312–321.

Woodruff, I., J.T. Kirby, F. Shi, and S. Grilli. (2018). “Estimating Meteo-Tsunami Occurreances for the US East Coast”. Coastal Engineering Proceedings, No. 36.