NUMERICAL SCHEME OF HIGHLY DISPERSIVE MODEL¶
Two-step projection method¶
A combined finite-volume and finite-difference scheme with a Godunov-type method was applied to discretize equation (Shi et al., 2012). The two-step projection method, which splits the time integration into a hydrostatic predictor phase and the non-hydrostatic corrector phase, is used within each R-K stage. In the hydrostatic phase, an intermediate quantity \(\bf{\Psi}^\prime\) is evaluated using the momentum equations with dynamic pressure term neglected. For the momentum equations, components 2,3,4 (refer to the theory).
In the non-hydrostatic phase, the velocity field is corrected using the momentum equations with only the dynamic pressure term included. The non-hydrostatic phase involves solving the Poisson equation of the dynamic pressure derived from coupling the momentum equation and mass conservation equation, resulting in the following equation of dynamic pressure
(151)¶\[\frac{\partial}{\partial x} \left [ \frac{\partial p}{\partial x}+\frac{\partial p}{\partial \sigma} \frac{\partial \sigma}{\partial x^*} \right ] + \frac{\partial}{\partial y} \left [ \frac{\partial p}{\partial y}+\frac{\partial p}{\partial \sigma} \frac{\partial \sigma}{\partial y^*} \right ]\](152)¶\[+ \frac{\partial }{\partial \sigma} \left ( \frac{\partial p}{\partial x} \right) \frac{\partial \sigma}{\partial x^*} + \frac{\partial }{\partial \sigma} \left ( \frac{\partial p}{\partial y} \right) \frac{\partial \sigma}{\partial y^*}+ \left[ \left (\frac{\partial \sigma}{\partial x^*} \right )^2+\left ( \frac{\partial \sigma}{\partial y^*} \right )^2+\frac{1}{D^2} \right] \frac{\partial }{\partial \sigma} \left( \frac{\partial p}{\partial \sigma} \right)\](153)¶\[= \frac{\rho}{\Delta t} \left( \frac{\partial u^*}{\partial x} +\frac{\partial u^*}{\partial \sigma} \frac{\partial \sigma}{\partial x^*} + \frac{\partial v^*}{\partial y} +\frac{\partial v^*}{\partial \sigma} \frac{\partial \sigma}{\partial y^*} + \frac{1}{D} \frac{\partial w^*}{\partial \sigma} \right)\]
After the dynamic pressure \(p\) is solved, the velocity field is corrected by
(154)¶\[\frac{{\bf \Psi}^{n+1} - {\bf \Psi}^*}{\Delta t} = {\bf S}_p^{n+1}\]
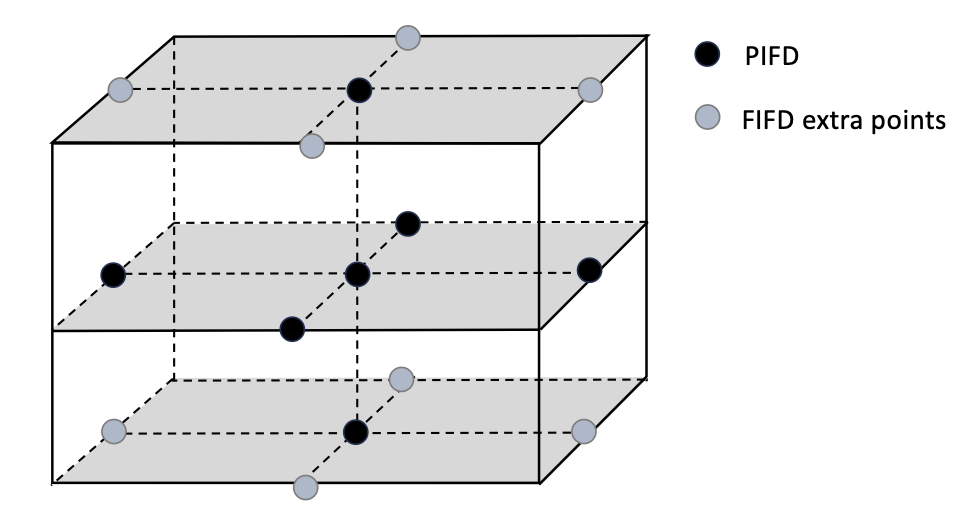
Partially Implicit Finite Difference (PIFD) scheme¶
A great challenge in a surface flow-type non-hydrostatic model is to solve the pressure Poisson equation, which is computational expensive. The recent studies have showed that the vertical grid configuration and construction of pressure value matrices are crucial for model efficiency and accuracy. The non-hydrostatic models using a Keller-box scheme in the vertical grid configuration (Stelling and Zijlema, 2003, Ma et al., 2012, Shi et al., 2016) were proved to be efficient and accurate in simulating highly dispersive waves with a very small number (3-5) of vertical layers. The re-arranging the Poisson equation to reduce the implicit values of the matrix has shown significant improvement of model efficiency. Liu et al. (2016) proposed a Partially Implicit Finite Difference (PIFD) scheme versus the Fully Implicit Finite Difference (FIFD) scheme by moving some minor terms from implicit to explicit evaluations in two steps. In the first step, the pressure gradient terms associated with the \(\sigma\)-derivatives are moved from the non-hydrostatic phase to the hydrostatic phase. In the second step, the cross-derivative terms in the pressure Poisson equation are solved explicitly. In this way, the 15-point of the solution matrix in FIFD reduce to a 7-point implicit matrix, improving the computational efficiency greatly. In this study, we followed the Keller-box scheme of Ma et al. (2012) and adopted the second step of PIFD in Liu et al. (2016). Our tests shows that the first step of PIFD is not necessary and the reconstruction of the solution matrix in the Poisson equation saves the similar amount of computational time as claimed by Liu et al. (2016), up to 50% compared to FIFD.
